Základy logaritmických rovnic: Matematická výzva vzdělávacího světa

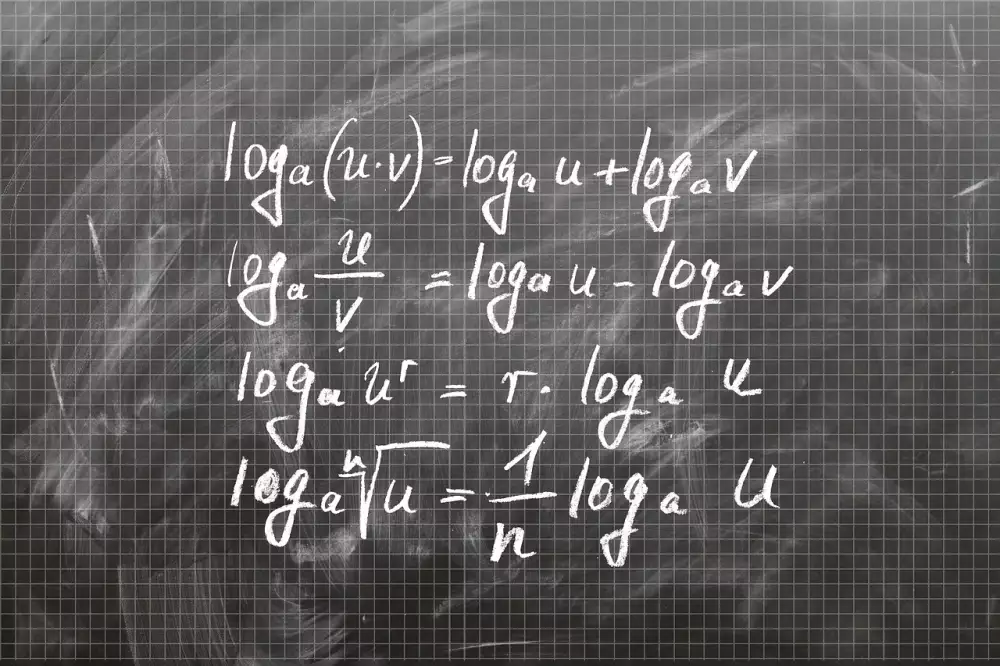
Logaritmy jsou matematická funkce, která je důležitá nejen ve fyzice a chemii, ale také ve výpočtech a statistice. Logaritmické rovnice jsou rovnicemi, kde neznámou veličinou je exponent logaritmu. Jejich řešení vyžaduje znalost základních pravidel a postupů. Logaritmické rovnice se často objevují při modelování různých jevů a procesů, a proto je důležité porozumět jim a umět je správně řešit. V tomto článku se zaměříme na základy řešení logaritmických rovnic a jejich aplikace v matematických problémech.

Základní pravidla pro řešení logaritmických rovnic.

Základní pravidla pro řešení logaritmických rovnic jsou klíčová pro správné pochopení jejich matematické podstaty. Prvním pravidlem je uplatnění základního vztahu logaritmu k mocnině: logₐ(b) = c je ekvivalentní s a^c = b. Druhým pravidlem je schopnost převést logaritmickou rovnici na exponenciální formu a naopak. Další důležité pravidlo je pamatovat si, že logaritmus z nuly neexistuje a logaritmus z jedničky vždy bude nula. Při řešení rovnic je také nutné dbát na platnost základních vlastností logaritmů, jako je součet logaritmů, rozdíl logaritmů a násobení či dělení logaritmovaných čísel.

Postup pro řešení logaritmických rovnic.

Postup pro řešení logaritmických rovnic začíná identifikací základu a exponentu v logaritmu. Poté se použije pravidlo, že logaritmus součinu je roven součtu logaritmů jednotlivých členů. Následně se aplikuje pravidlo, že logaritmus podílu je rozdíl logaritmů dělitelů. Dalším krokem je převést rovnici na exponenciální tvar a vyřešit ji. Nakonec se ověří nalezené řešení dosazením zpět do původní rovnice. Tento postup umožňuje systematicky a správně řešit různé typy logaritmických rovnic.

Příklady řešení logaritmických rovnic krok za krokem.

Představme si logaritmickou rovnici: log₃(x+2) = 2. Nejprve se zbavíme logaritmu pomocí základního pravidla, tedy převedeme ji na mocninový tvar: 3² = x+2. Dostaneme tak rovnici 9 = x+2. Nyní stačí jednoduše vyřešit rovnici pro x a zjistíme, že x = 7. Tím jsme úspěšně vyřešili danou logaritmickou rovnici krok za krokem. Takto postupujeme i u dalších příkladů, kde aplikujeme základní pravidla logaritmů a postupně řešíme rovnice a hledáme neznámé proměnné.

Aplikace logaritmických rovnic v matematických problémech.

Logaritmické rovnice mají široké uplatnění v matematických problémech a reálném světě. Například v biologii se logaritmy používají k modelování růstu populace nebo radioaktivního rozpadu. V ekonomii jsou logaritmy důležité pro výpočet úroků, inflace nebo pro analýzu tržních trendů. V fyzice se logaritmické rovnice využívají například při studiu akustiky, optiky nebo při analýze elektrických obvodů. Logaritmy jsou klíčovým nástrojem pro řešení složitých matematických problémů napříč různými disciplínami.

Závěrem lze konstatovat, že logaritmické rovnice představují důležitou součást matematického vzdělání a mají široké uplatnění v různých oblastech. Jejich porozumění a správné řešení vyžaduje pevné znalosti matematických pravidel a postupů. Logaritmy jsou nezbytným nástrojem například při modelování různých jevů ve fyzice, chemii či ekonomii. Díky nim lze efektivněji řešit složité problémy a analýzy, což studenty připravuje na praktické využití matematiky v reálném světě. Logaritmické rovnice tak rozvíjejí analytické myšlení a matematickou gramotnost, která je klíčová pro úspěch ve studiu i v profesním životě.